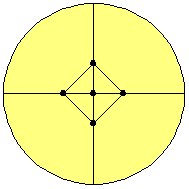
図2. 射影平面上の 4 -正則グラフ
球面上の対心点の組を 1 点に同一視することで得られる閉曲面を 射影平面と呼ぶ. 3 次元空間の中で射影平面を実現することはできないが, 無理に絵を描くと,図 1 のような外形になる.
図1. 射影平面
このウルトラマンの頭のような形にこだわらずに, 次のように考えると,射影平面がわかったような気になれる. まず,球面の北半球に注目しよう. どの対心点の組においても,その一方の点が北半球に属している. どうせ対心点の組は 1 個の点になってしまうのだから, 南半球にある方を忘れて,北半球の点にその組を代表してもらおう. さらに,半球のままだと扱いにくいので, その北半球を平らにして,平面上の円板だと思ってしまう. このとき,その円板の周囲はもとの球面の赤道に対応していることに注意しよう.
単に平面上の円板なら,絵を描くのは簡単である. ただし,円板の周上に並ぶ点は, 円板の中心に関して対称な位置にある点と同一視されなければならない. つまり, その円板の中を外に向かって進んでいって円周に到達したら, 次の瞬間には,円周上の真反対の点にワープしなければならないのである.

図2. 射影平面上の 4 -正則グラフ
例えば,図 2 にある円板を射影平面だと考えよう. そこには,黒丸が 5 個描かれていて,互いに線で結ばれている. それぞれ上下左右に伸びている線は円周で分断されたようになっているが, 上で述べたワープの規則に従うと, 上に伸びている線は実は下の線とつながっていることになる. 左右の線についても同様である.
こう考えると,黒丸と太線からなる部分は 5 個の点と 10 本の線からなる グラフになっている. さらに,その各点からは 4 本の線が出ている. このように,どの点からも 4 本の線が出ているグラフを 一般に 4-正則グラフという.
射影平面に限らず, 閉曲面上に描かれた 4-正則グラフに付随する双対グラフを考えよう. それは,各領域の中心に点を置き,もとのグラフの線を挟んで接している領域に 置かれた点を線で結んで得られるグラフである.
逆に,双対グラフの各領域はもとのグラフの点を含んでおり, その点から伸びている線が双対グラフの領域の境界線と交差している. ということは,どの点からも 4 本の線が出ているならば, 双対グラフのどの領域の境界も四角形になっているのである. つまり, 4-正則グラフの双対グラフは, それが描かれている閉曲面の四角形分割になっている.
これで仁野さんの「射影平面上の 4-正則グラフ」の研究が 中本君の「閉曲面上の四角形分割の対角変形」の研究に 関連している理由がわかっただろう.
ところで, 上で述べたワープの規則に従って射影平面を表わす円板の中を旅行すると, 円周を横切るたびに,左右がひっくり返ってしまうことがわかるだろう. ということは,この射影平面の世界では, 右や左という概念をその世界の全域にわたって矛盾なく 定義することができない. このように,左右の概念を定めることのできない世界のことを 向き付け不可能であるという.