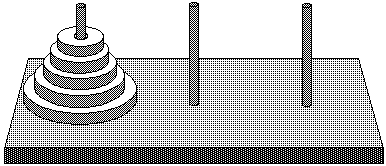
図1. ハノイの塔
そして,数日が過ぎた. 学内の雑事に追われ,会議の日が続き, ハノイの塔のメールのことはすっかり忘れていた.
ところが,ある日のこと, あの愉快犯の張本人とおぼしき人物から, 私個人宛に電子メールが届いたのである. その人の名前が英語圏のものとは思えないようなものだったことと, 後に起こった事件により, そのメールが消滅してしまったことから, その人の名前を思い出すことができないのが残念である. それでは不便であるから, 彼のことを「ハノイの塔」にちなんで, 仮に「ハノイ氏」と呼ぶことにしよう.
そのメッセージはもちろん英語で書かれていたが, あまりうまい英文だとは言いがたかった. その内容は,概ね次のようなものと記憶している.
このメールを読んで, これをどう捉えたらよいのかと, 傍らのマウスを握りしめたまま,しばらく空中を眺めていた. そして,とりあえずの応答として,次のようなメッセージを送った.
今思えば,無愛想な返事だった. そのためか,数日待っても,ハノイ氏からのさらなるメッセージは来なかった.
しかし,ハノイ氏はどうして私のところに直接メッセージを送ってきたのだろうか? そもそも,どうして 私が「ハノイの塔が崩壊した」のメッセージを 受け取ったことが,彼にわかったのだろうか? 彼が直接発信したメールの着信状況を知ることは可能だろう. さらに何人も乗り継いでメールが誰に届いたのかまで知る術が 現在の電子メール・システムにはあるのだろうか?
プライバシーの問題などを考えると, そのような仕組みがあることは想像しがたいが, 事実,ハノイ氏は私の電子メール・アドレスを入手し, 私に直接メッセージを送ってきたのである.
まあ,私もその道ではそれなりの有名人だし, 学術雑誌に掲載されている私の論文を見れば, 私の電子メール・アドレスも書いてあるのだから, 彼が私に直接メールを送ってきたからとて,不思議ではない. 現に,外国人に限らず, 見ず知らずの人からメールが届くことがよくあるではないか….
とはいえ,ハノイ氏の電子メールはなぜか気になった. そもそも,彼のメッセージはどういう意味なのだろうか? ハノイの塔が壊れたから,それを直す方法を考えろという. 単に物としてのハノイの塔が壊れたのなら, 数学者の責任で考えるような問題ではない. もしそうなら,文房具屋に行って,接着剤を買ってくればよいではないか.
少なくとも私は,彼のメッセージを数学者に向けて発信した 数学の問題なのだと解釈することにした. だとすると,彼の出題の仕方はかなり曖昧である. もちろん,多少曖昧な問題を解答者の判断で適宜解釈して, おもしろい問題にして答えを示すということがないわけではない. しかし,相手と直接会話を交わすことができない 電子メールで通信を行う場合には, 双方に自分のメッセージが一義的に解釈できるように気を使って 作文するのがエチケットというものである.
そういう私も,ハノイ氏の意図を確認することを怠り, 適当にあしらうような返事を送ってしまった. いまさら,問題の意味を聞くこともできない. しかたがないから, 自分なりにその問題を考えてみることにした.
そもそも,ハノイの塔をご存じない人もいるだろうから, 簡単にそれを説明しておこう.

図1. ハノイの塔
問題はこの初期状態から始めて,すべての板を棒 2 に移動せよというもの. ただし,小さい板の上にそれよりも大きい板を積んではいけない. 必要ならば,どの棒に板を移動してもよい. このルールを守りながら, 板を 1 つずつ移動して,すべての板を棒 2 に大きい順に積み上げろというのが このパズルの問題である.
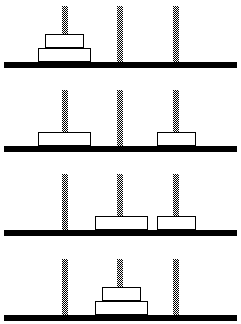
図2. 2 段のハノイの塔の解法
これがわかれば, 3 段のハノイの塔もそれほど難しくない. くどくど説明せずに,その手順だけを示すと次のとおりである. 動かす板の番号が書かれていないが, もちろん, その棒に刺さっている一番上の板を動かせばよいのである.
ついでに, 4 段のハノイの塔の解法も示しておく. パズル好きの人は自分で答えを探すのもよいが, 手数が多いので,少々手間取るだろう.
この指示どおりにやってみるとわかることだが, それは決して偶然に支配された解法ではなく, 何らかの規則性が存在しているような感触がある. それは何かの繰り返しのような気がする. しかし,それはストレートにこれとは言いにくいものになっている. というのも, このハノイの塔の解法はいわゆる“再帰的な”構造を持っているからである.
その再帰的構造については,いずれ解説することになるだろう. ここでは,ハノイの塔を解くのに必要な手数の評価を試みよう.
すでに示したような 個々の段数のハノイの塔の解法を眺めていても, なかなかその解法の一般形が見えてこない. そこで,思いきって次のような抽象的な議論を決行する.
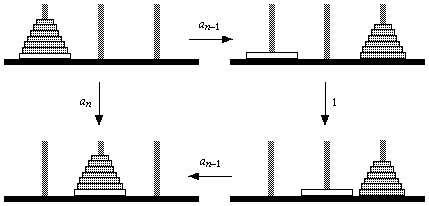
図3. ハノイの塔の再帰的解法
まず, n 段のハノイの塔の手数を an と書くことにする. 例えば,すでにわかっているところでは, a1 = 1 , a2 = 3 , a3 = 7 , a4 = 15 である. これを見て, an の正体がわかってしまったら, あなたはかなり冴えている. 答えを先に述べてしまえば, n 段のハノイの塔には 2n - 1 回の板の移動が必要十分なのである. つまり, an = 2n - 1 である. 確かに, 2 , 4 , 8 , 16 という 2 のべき乗 から 1 を引くと, a1 , a2 , a3 , a4 の値になっている.
さて,ここに n 段のハノイの塔があったとしよう. 初期状態では,棒 1 に板 1 から板 n までの n 枚の板が 大きい順に積み上げられている. ということは, 一番下の板 n を無視すれば, n-1 段のハノイの塔があると思える.
最終的には,棒 2 に初めと同じ順番で n 枚の板を積み上げるのだから, ある時点で板 n が棒 2 に移動しなければならない. その移動ができるためには, 棒 1 にある板 n の上には何もなく, さらに移動先の棒 2 にも他の板があってはならない. なぜなら,板 n は一番大きいのだから, その下には他の板を置くことができないからである.
ということは,板 n を移動しようとするときには, 板 1 から板 n-1 まではすべて棒 3 に移動していることになる. さらに,小さい板の上には大きい板を乗せられないのだから, 棒 3 にはその n-1 枚の板が大きい順に積み上げられているのである. その状態を最小手数で実現しようと思うなら, n-1 段のハノイの塔の解法を実行すればよい. ただし,板の移動先が棒 3 であるから, 棒 2 と棒 3 の役目を入れ替えて考える必要はある.
したがって,板 n を移動する直前までに n-1 段のハノイの塔の解法と 同じ手数の板の移動があったことになる. その手数は an-1 である. それに板 n の移動の 1 手を加えて, an-1 + 1 . あとは,棒 3 にある n-1 枚の板を棒 2 に移動した板 n の上に積み上げれば, ハノイの塔の移動が完成する. その作業も棒の役目を入れ替えて考えれば n-1 段のハノイの塔の移動に他ならない. すなわち,さらに an-1 回の板の移動を行えば,すべてが完成することになる. (図 3 参照)
これで, n 段のハノイの塔の解法には, 通算 an-1 + 1 + an-1 回の板の移動が必要であり, 十分であることがわかった. これから,次の漸化式が得られる.
この漸化式を解いて an の一般形を求めるのは簡単である. まず,第 2 式の両辺に 1 を足してみよう.
この式は, n が 1 つ大きくなるたびに, an + 1 が 2 倍になっていくことを意味している. となれば, a1 + 1 = 2 だから, 2 から始めて 2 倍, 2 倍を繰り返していけば, n 回目には an + 1 = 2n となる. これから, an = 2n - 1 が得られるわけだ.
かくして, n 段のハノイの塔の解法に必要な手数が 2n -1 であることがわかった. 待てよ. これは何かと似ていないか? そうである. 2n - 1 はまさに ハノイ氏から n 人以内の人手を経てメッセージを受け取った人の人数 に他ならない. これは偶然の一致なのだろうか? それとも,これもハノイ氏の仕組んだことなのだろうか?
いずれにせよ,ハノイの塔の解法に必要な手数が ハノイ氏からのメッセージの受取人の人数と同じだということは, 後者と同様に, ハノイの塔の段数が少しでも大きくなっただけでも, その手数は爆発的に増大することになる. つまり,その手数の 2n - 1 はそれほど大きくない n の値に対しても, 莫大な数になってしまうのである. たった 10 枚の板を積み上げたとしても, それをルールどおりに隣の棒に移動するには, 210-1 = 1023 回の板の移動が必要なのである. それが 100 段の板を積み上げたハノイの塔だったら….
そんなハノイの塔が崩壊した姿を目の前にして, それを修復せよと言われたとしたら, いったい何ができるというのだろうか? その修復に必要な手数に圧倒されて, ただ途方に暮れるだけではないだろうか. はたして,ハノイ氏のいうところの, ハノイの塔の崩壊,そして修復とは, 何を意味しているのだろうか?