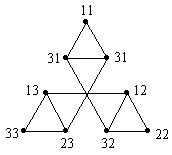
図 1. 2 段のハノイの塔の全状態図
田沼君が私に話してくれたことを記しておこう. それは,ハノイの塔の手順には現れない状態があるというものだった.
まず,小さい板の上には大きい板を乗せないというルールを守って n 枚の板を積み上げてできあがるハノイの塔の状態の総数を考えよう. ルールを破らずに板を積んでいくには, 一番大きい板から小さい板へと順に棒に刺していけばよい. このやり方で板を積んでいくかぎり, それぞれの板を積むときに, どの棒に刺さなければいけないという制限は何もない. つまり,次の 1 枚の積み方は,棒 1 ,棒 2 ,棒 3 のどこに積んでもよいので, 3 通りである.
ということは, 板 n を積むのに 3 通り, そのそれぞれの場合について,板 n-1 を積むのに 3 通りだから, 3 × 3 で,合計 9 通り. さらに,板 n-2 を積むのに, 9 通りのそれぞれの場合について 3 通りで, 合計 3 × 3 × 3 = 27 通り. こう考えていくと, すべての板を積む積み方の総数は, 3 を n 回掛けた 3n 通りであることがわかる.
一方,ハノイの塔の移動過程に現れる状態は, その手数の 2n - 1 に初期状態の 1 を加えた 2n 通りである. この 2n 通りの状態は,当然,すでに考えた 3n 通りの状態のうちに含まれている. その移動の初期状態は n 枚の板がすべて棒 1 に刺さっていて, 終了状態では棒 2 にすべての板が刺さっている. 反対に,棒 2 から棒 1 にハノイの塔を移動しようと思うならば, 棒 1 から棒 2 への移動の逆の過程をたどればよいことになる. 棒 1 から棒 3 に移動する場合も, 棒 2 と棒 3 の役割を入れ替えて考えれば, 同様の 2n 通りの状態を経て移動が完了する.
移動の方向(棒 i →棒 j )は全部で 6 通りあるが, 逆方向はたどる順番が逆なだけで,通過する状態は共通である. こう考えると, 1 ←→ 2 , 1 ←→ 3 , 2 ←→ 3 の 3 組の移動に対応して, それぞれ 2n 通りの状態が存在する. それを併せて 3 × 2n とすると, 明らかに初期状態の重複があるから,その分を引いておこう.
したがって, 仮に,初期状態以外の重複がなければ,次の不等式が成り立っているはずである. 3 × 2n - 3 ≦ 3n この不等式の n に 1 から順に値を入れて確かめてみると, n = 1, 2 のときには等号が成立するが, n ≧ 3 のときには不等号しか成立しないことがわかる. 3 × 2n - 3 < 3n (n ≧ 3) この不等式は,ハノイの塔の移動過程の状態に対応させて数えたのでは, 数え残してしまう状態があることを意味している.
「なるほどね. これで,ハノイの塔の手順に現れない状態があることはわかったよ. で,それは具体的にはどういう形なの?」
「それはですねぇ,状態を全部書き下してみないと,わからないんですけど….」
「なんだ,なんだ. 3n 通りもの状態を全部書き下すなんて, 無謀じゃないか.」
「いえいえ,先生.それがですねぇ,うまい方法があるんですよ.」
そういって,田沼君は黒板に三角形を描き, その頂点に 1 , 2 , 3 と番号を書いた. そして,それが 1 段のハノイの塔の全状態を表す絵なのだと言った.
その絵は簡単すぎるので,あまり意味はないが, その番号は板 1 がそれぞれ棒 1 , 棒 2 ,棒 3 にいる状態を表しており, 1 手で移り合える状態に対応している頂点どうしが線で結ばれている. それと同じ意味になるように, 2 段のハノイの塔の場合の絵を描くと, 図 1 のようになる.

図 1. 2 段のハノイの塔の全状態図
各頂点(黒丸)には 2 桁の番号が添えられているが, その各桁の番号はその桁に対応する板が刺さっている棒の番号になっている. 例えば,一番上,右下,左下の頂点には 11 , 22 , 33 と書かれているが, それは板 1 と板 2 の両方ともが それぞれ棒 1 ,棒 2 ,棒 3 に刺さっていることを表している. つまり,ハノイの塔の初期状態に対応しているわけだ.
その番号付けが示唆しているように, その 2 段のハノイの塔の全状態図には次のような うまい構造があるのだった. 例えば,頂点 11 を含む図の天辺に位置する三角形に注目しよう. この三角形の中では,どの頂点の 2 桁目も 1 になっている. つまり,それは板 2 が棒 1 に刺さっている状態に対応している. さらに,その数字の 2 桁目を無視すれば, その三角形は上で述べた 1 段のハノイの塔の全状態図になっている. もちろん,右下,左下の三角形の番号付けも, これと同じ仕組みになっている.
「ところで,なぜ,そんな交差があるような絵を描くんだい. そこのところを捻れば,交差が解消するじゃないか.」
「いえいえ,先生.それじゃだめなんですよ. こういうふうにしておくから, 1 段のハノイの塔の全状態図が 3 ヶ所にうまく納まっているんですよ.」
「なるほど.」
「この考え方を使えば, 3 段のハノイの塔の全状態図だって, 簡単に描けちゃうんです.」
そう言って,田沼君は, 2 段のハノイの塔の全状態図のコピーを 3 つ三角形状に並べて描き, 3 本の線を追加した. そして, 各頂点に 3 桁の番号を書いていった.
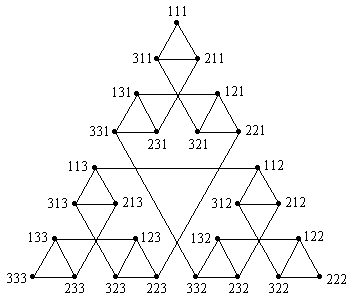
図 2. 3 段のハノイの塔の全状態図 1
1 つの 2 段のハノイの全状態図の中に限れば, 各番号の初めの 2 桁までは以前のものと同じで, 3 桁目が共通になっている. 確かに,私が指摘した交差の解消を行わない方がよいようだ. 番号付けの構造が保存されるから, 田沼君のやり方は合理的だといわざるをえない.
さらに,田沼君は黄色のチョークを持って, 頂点 11 , 22 , 33 を結ぶ 3 本の道(図 3 の太線)を書き込んだ. それがハノイの塔の移動の過程を表しているのだ. そして,その道が通らない 6 個の頂点を丸で囲んだ. その頂点に対応する状態が,ハノイの塔の手順に現れない状態というわけである. 例えば,頂点 121 がそういう頂点である. これに対応して,板 1 と板 3 が棒 1 にあり,板 2 が棒 2 にある状態が ハノイの塔の手順には現れないことがわかる.
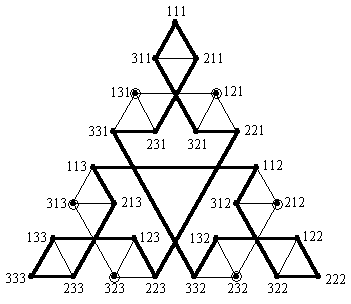
図 2. 3 段のハノイの塔の全状態図 2}
「なかなか,うまくできているね.」
「てへへ.そうでしょう.このやり方を繰り返していけば, 何段のハノイの塔の全状態図だって描けていって, 無限に広がっていってしまうんです.」
確かに, 2 段や 3 段のハノイの塔の個別的な議論を超越して, 私たちの理解は無限に広がっていった. そのおかげで, 最初の不等式を立てるときに考えた「初期状態以外に重複がない」という仮定が, もはや仮定ではなく,事実であることが理解できたのである.
まあ,これも「形」から「言葉」への移行の結果と言えるだろう. めでたし,めでたし.