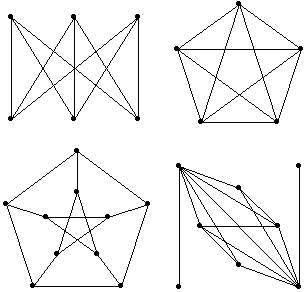
図1. グラフいろいろ
図 1 にあるような, 点と線からなる図形をグラフと呼ぶ. それは関数のグラフとは無関係である. そのグラフを対象に行われる研究がグラフ理論である. 偉大な数学者であるR. オイラーが一筆書きの問題を扱った 1786年の論文とともにグラフ理論が始まったと言われているが, 地図の色分け問題や四色問題などの研究が原動力となって, 20 世紀に急成長を遂げた. データ構造やアルゴリズムの題材に使われるなど, コンピュータ・サイエンスとの関係も深い.

図1. グラフいろいろ
通常,離散数学,組合せ理論の一分野として位置づけられているが, グラフの幾何学的側面に焦点を当てた研究も行われている. ちなみに,私の専門は「位相幾何学的グラフ理論」といって, グラフ理論の中でも位相幾何学(トポロジー)と結合した分野である. その詳細は後述する.
導入が容易で,パズル的な問題が多いことから, グラフ理論を低級で体系のない数学だと思い込んでいる古い数学者も少なくない. しかし,今日の発展した姿を無視して,そのような発言をするとしたら, 極めて恥ずかしい思いをするだろう. 現状では,学校数学の中にまったく姿を現していないため知名度は低いが, グラフ理論は情報科学関連の大学では必須の科目として指導されている.
グラフ理論について一通りのことを学びたければ, 次の本を参考にしてほしい.
また,インターネットに接続されたパソコンをお持ちの方は 私のホームページ