私は足に任せて本屋街を立ち去った． 秋葉原から本屋街に来たコースを逆にたどり， 営団地下鉄の新御茶ノ水駅に向かった．

　その改札口まで私を運ぶエスカレーターは恐ろしく長い． そして，いつもなら高所恐怖症の私はその高低差に緊張しているはずだった． しかし，そのときの私にはその高低差など無関係だった． 私の意識のどこかはそれを恐怖していたのかもしれないが，私は感知していない． というのも，エスカレーターは下りだったが， 私は今開けたばかりの扉の向こうにある階段を昇り始めたところだからだ．

　切符を買い，プラットホームに行き，電車を待ち， 電車が来たらその動きに注意を払い， ドアが開けば乗り込んで， 車両の連結部の近くの空いている席に座り， 背負っていたリュックサック状の鞄を膝の上に置く． そういう一連の行動を機械的に済ませた私は， 鞄の中から紙と鉛筆を取り出した．

　電車が少し動き出してから， 隣の車両から大学生らしい女の子がやってきて，私の前に立った． そして，ためらいがちに次の言葉を言った．

「あなたの健康と幸せをお祈りさせてください．」

　普通の人にとってこの台詞は異様なものだろうが， そのときの私の雰囲気の方がよっぽど異様だったにちがいない． 彼女を見ているとも見ていないとも思える視線に恐怖して， 彼女はその場を去っていった． さらに，その後を追うように 2 人の男たちが隣の車両から歩いてきて， 私の前を通り過ぎていった． その男たちは彼女の行動を監視しているのだなと私は直感した． 彼女も怪しげな宗教団体の犠牲者なのかと思ったが， 今の私にはどうでもよいことだ．

図5. ハノイの塔の解明図 1

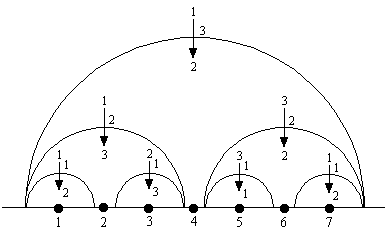
　かくして，ハノイの塔の解明図１が描かれることになる． 最終的に描かれた黒丸は，半円のつなぎ目に位置するものも合わせて全部で 7 個． 左から順に 1 から 7 までの番号を振っておこう． この時点ではまだ矢印は書き込まれていない． その意味は追って説明するとして， この形をよーく観察してみよう． 確かに，この図は曼陀羅に始まり最終的に到達した イデアル三角形の図に酷似している． いったい，この入れ子の半円の図は何を意味しているのだろうか？

　少なくとも，この解明図が 7 手を必要とする 3 段のハノイの塔の移動に 相当していることは明らかだろう． そして，水平に引いた直線は時間軸のように思える． となれば， 1 から 7 までの番号を振られた黒丸は， それぞれその番号の値を手数とする板の動きに対応しているにちがいない．

　なるほど． そう考えると，この図の意味がわかってくるぞ． 一番外側の半円が 3 段のハノイの塔の移動の全過程をくくっているのだ． その中に置かれた左の半円は初めの 3 手を， 右の半円は最後の 3 手をくくっている． そして，そのつなぎ目の黒丸はちょうど真ん中の 4 手目に対応している．

　では，その 4 手目は何に対応しているのか？ それは一番大きな板 3 が動く瞬間だった． そして，その 4 手目に着手する前には， 板 3 を無視した 2 段のハノイの塔が棒 1 から棒 3 に移動して， 4 手目の実行後に，その 2 段のハノイの塔が棒 3 から棒 2 に移動するのだった．

　実は，半円を上から下に横切るように描かれた矢印とそれに付随する数字は， この状況を表わしているのである． つまり，その矢印が指している黒丸の番号が手数で， 矢印の中央に添えられた数字がそのときに動かされる板の番号であり， その板が矢印の始点の番号の棒から終点の番号の棒に移動する．

　さらに，小さい半円を横切る矢印の番号も同様に解釈することができる． 左の半円は 2 段のハノイの塔を棒 1 から棒 3 に移動することに 対応しているのだから， それを横切る矢印には板の番号の 2 と移動元，移動先の棒の番号の 1 と 3 が 添えられている． 右の半円についても，同様である．

　これで，この解明図が本当に 3 段のハノイの塔を 解明したものであることがわかった． その仕組みが理解できれば， 何段のハノイの塔の解明図でも原理的には描けることになる． とはいえ，段数が多くなれば， 描かなければならない半円の個数は指数関数的に増加してしまい， 実際にそれを書き下すことは事実上不可能である． それならば，解明図の具体的な形には執着せずに， 少し抽象的に考えてみることにしよう．

　まず，この解明図の基本となる構造は， 大きな半円とその中に納まる 2 つの半円， それに，その 2 つの半円をつなぐ黒丸である． 段数が多くなれば， この構造が小さな半円の中へと繰り返されていき， 描かれる半円や黒丸の個数が増加していく．

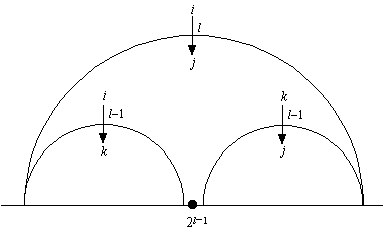
図6. ハノイの塔の解明図 2

　その大きな半円を横切る矢印に付随する l , i , j は， その半円が板 l とそれより上の部分からなる l 段のハノイの塔を 棒 i から棒 j に移動する過程に対応していることを意味している． 特に，その矢印が指している黒丸は， その移動過程の中では 2^l-1 手目に対応している． ただし，ハノイの塔の移動の全過程の中では，ちょうど 2^l-1 手目であるとは かぎらない． その半円が置かれる位置に応じて， それに何手かを加算した値が本当の手数である．

　あくまでこの l 段のハノイの塔の移動過程だけに言及すると， 板 l が移動可能になるためには， それよりも上の部分からなる l-1 段のハノイの塔を 棒 i から棒 k に待避させる必要がある． ただし， k は 1 , 2 , 3 のうち， i でも j でもない番号である． この待避作業を表わすように， 左の半円を横切る矢印には l-1 ， i ， k が添えられている． また，右の半円は，棒 k に待避しておいた l-1 段のハノイの塔を棒 j に移動する 過程に対応している． それを表わすように，その半円を横切る矢印には l-1 ， k ， j が添えられている．

　そもそもハノイの塔の全体は棒 1 から棒 2 に移動することになっていたから， その全過程を表わす解明図において，一番外側の半円を横切る矢印には ハノイの塔の段数の n が添えられ， その始点には 1 ，終点には 2 が書かれている． その状態から始めて，解明図２のルールに従い， 左右の半円，黒丸，矢印，それに添える番号を描き込んでいけば， 解明図が生成できることになる．

　これで何とは言いにくかったハノイの塔の移動過程が， ビジュアルな形あるものに昇格した． さらに，その基本構造が言葉で表現できるようになった． これでハノイの塔のすべてが目の前に現れたような気がする． それならば，あの「ハノイの塔を修復せよ」 というハノイ氏の問題も， 解明図を理解することで， 簡単に解決できるにちがいない． つまり，与えられた手数において， どの板がどの棒に刺さっているのかを特定するのである．

　いずれにせよ，解明図それ自体が示唆してくれているように， 一番外側から矢印に沿って移動して，半円の中へ中へと進んでいくことを考えよう．

　今， n 段のハノイの塔の m 手目の状態が知りたいものとしよう． このとき，最初にたどる矢印は 1 -- n --> 2 となっており， その矢印が指している黒丸には番号 2^n-1 が振られているだろう． これは次のことを意味している．

　まず， m < 2^n-1 ならば，板 n はまだ棒 1 にあり， 板 n を無視した n-1 段のハノイの塔を棒 1 から棒 3 に 待避させる作業を実行中である． m = 2^n-1 ならば，ちょうど板 n を棒 1 から棒 2 に移動するところで， それができるように，板 n を無視した n-1 段のハノイの塔は すでに棒 3 に待避済み． つまり，この場合には，この時点ですべての板の位置がわかる． 最後に， m > 2^n-1 ならば，板 n は棒 2 に移動済みである．

　これで板 n の位置が確定した． m = 2^n-1 の場合には，すべての板の位置が確定しているが， そうでない場合には他の板の位置を確定するために， さらに考察を続ける必要がある．

　 m < 2^n-1 の場合は， m 手目に対応する黒丸は真ん中よりも左に位置しているので， 左の半円の中へと進んでいく． その半円は n-1 段のハノイの塔を棒 1 から棒 3 へ 待避させる作業をくくっているのだから， 今と同様に，その半円を横切る矢印に添えられた番号を見れば， 板 n-1 がどこにいるのかがわかる．

　一方， m > 2^n-1 の場合には， 待避しておいた n-1 段のハノイの塔を棒 3 から棒 1 に移動している最中である． その状況は右の半円を横切っている矢印が表わしていて， そこに添えられている番号を見れば，板 n-1 が今どこにいるのかが判断できる． いったん右の半円に入ってしまえば，外に出てくることはないのだから， 手数をその半円の始まりの位置（左端）を基点として数え直して 以後の考察を続けた方が便利である． つまり，その右の半円に対応する移動を始めるまでにすでに 2^n-1 手を 費やしているのだから， その基点から数えた手数は m - 2^n-1 である．

　左にしろ，右にしろ，さらに半円の内部に進入しながら， 同様の考察を繰り返していけば， 番号の小さい板の位置も確定していくことがわかるだろう． そして，矢印が直接黒丸を指している状態になった時点で， すべての板の位置が確定する． そうなるまでに，左に行ったり，右に行ったりを繰り返すが， 右の半円に進入するたびに， m の値は相対的なものに置き換えられて小さくなっていく． 最終的にその値が 2 のべき乗の形になったときに， 矢印が黒丸を直接指す状態になるのである．

　結局のところ，段数が多くなれば解明図が複雑になるにしても， 繰り返されることはいつも同じである． それを半円の存在を無視して書き下すと，次のようにまとめられる． l の初期値を n として， l を 1 ずつ小さくしていきながら， これを繰り返していけば，大きい板から順に，その位置が特定されていくのである．

• m = 2^l-1 の場合
  板 l が棒 i から棒 j に動く．
  板 1 から板 l-1 までは棒 k にある．
  すべて決着．

• m < 2^l-1 の場合
  板 l は棒 i にある．
  板 1 から板 l-1 までを棒 i から棒 k に移動中．
  移動先 j を k と入れ換える．

• m > 2^l-1 の場合
  板 l は棒 j にある．
  板 1 から板 l-1 までを棒 k から棒 j に移動中．
  m を m - 2^l-1 に置き換え， 移動元 i を k と入れ換える．

「やった！」

　はたして心の中の叫びだったのか，声を発したのか？ 一つの区切りを得て，私は通常のモードに切り替わった． ふと外界の様子を観察すると， 地下鉄の乗客たちは私の動きに反応している様子ではなかった． もし私が無音の叫び声を上げていたのなら， もちろん誰もそれに気づくわけもない． そうでないとしても， 彼らはおかしな人間には関わらないという都会人の原則を守っているだろう．

　いずれにせよ， 私の頭の中から，無駄なエントロピー がシューシューと音を立てて放出され， 私の身体からはみ出ていたオーラが中に引きずり込まれていくのを感じた． そして， 1 つの安定状態を迎える．

　この安定状態を迎えた後は， 普通の人たちが数学だと思っている活動が始まる． つまり，自分の発想の正当性を冷静にチェックするのである． 高校生たちが思い込んでいる「数式を計算する」 という数学のイメージとは異なるが， 獲得した結論が論理的な演繹のスタイルで表現可能かどうかを判定するのである． とはいえ，あくまでもそれは形式的な行為であり， 数学を創造するという意味においては本質的なことではないのだが…．